Research Discussion Paper – RDP 2019-05 Cost-benefit Analysis of Leaning against the Wind
July 2019
1. Introduction
‘Leaning against the wind’ is the policy of setting interest rates higher than a narrow interpretation of a central bank's macroeconomic objectives would warrant due to concerns about financial instability. This policy aims to dampen large increases in credit and asset prices. It is supported by a large literature that finds that ‘sustained rapid credit growth combined with large increases in asset prices appears to increase the probability of an episode of financial instability’ (Borio and Lowe 2002).[1]
However, there are also costs of leaning against the wind, such as lower income and employment. Following Svensson ((2017a), though most of the literature cites earlier versions), numerous papers have extended the earlier research by quantifying and comparing both the costs and benefits of leaning against the wind. This is part of a broader trend to base economic policy on empirical cost-benefit analysis (Sunstein 2018). The main objective of this paper is to summarise the new research on leaning against the wind and discuss how it might be applied to Australia. We also discuss several concerns that have been raised regarding the research.
The new research assumes that the main benefit of leaning against the wind is avoiding financial crises, defined as episodes of substantial bank failures, such as the global financial crisis of 2008. Australia has experienced two of these crises – in 1893 and 1990. An advantage of this definition is that it enables both benefits and costs to be measured in terms of expected changes in unemployment. A debatable disadvantage of this definition is that it may be too narrow. As discussed below, the Reserve Bank of Australia (RBA) has broader objectives.
This benefit can be measured as the product of a lower probability of a financial crisis and the likely size of that crisis. Estimates of the lower probability of a crisis are based on (i) the effect of interest rates on credit growth, and (ii) the effect of credit growth on the probability of a crisis. Estimates of the effect of interest rates on credit growth are generally taken from simple regressions or vector autoregressions (VARs), while estimates of the effect of credit growth on the risk of a financial crisis are generally based on Schularick and Taylor (2012) or similar databases. The size of the financial crisis, usually measured by the expected increase in the unemployment gap, is assumed to be similar to past crises. This can then be compared with estimates of the effect of interest rates on the unemployment rate taken from, for example, a structural macroeconomic model. A quadratic loss function is typically assumed, and prudential policy is assumed to respond as it has in the past.
In many papers, this approach leads to the conclusion that some degree of leaning against the wind can raise welfare. The reason is that the conventional welfare costs of small deviations from the macroeconomic optimum are close to zero. Leaning against the wind involves incurring this negligible cost in return for a reduction in the probability of a crisis in the future, so would, on net, be beneficial. However, estimated magnitudes are tiny. Ajello et al (2016) estimate the welfare-maximising level of leaning against the wind involves raising interest rates by 3 basis points; this is ‘in line with’ the results of Aikman et al (2018); while Pescatori and Laséen (2016) estimate it to be 6 basis points. For larger, more relevant deviations, the costs of leaning against the wind increase to be substantially greater than the benefits. Pescatori and Laséen find that a 25 basis point increase in the Canadian policy rate would reduce welfare by 0.4 per cent. Svensson (2017a) finds costs exceed benefits by ‘a large margin’. In the ‘average probability’ scenario of the International Monetary Fund (Habermeier et al 2015, p 25), the welfare cost of a 100 basis point increase in the policy rate is around 30 times larger than the benefits. Gorea, Kryvtsov and Takamura (2016) estimate costs are 20 times benefits (taking midpoints of baseline ranges). Kockerols and Kok (2019, Figure 1) estimate that costs for the euro area would be three times as large as benefits. Specchia and Plank (2017) provide simple estimates for Australia, concluding that costs may exceed benefits.
The most common result of the research is that the costs of any meaningful leaning against the wind outweigh the benefits. This assessment is shared by other overviews of the research including Bernanke (2015), FOMC (2016, pp 2–3), Bank of Canada (2016, p 27), Allen, Bean and De Gregorio (2016, pp 19, 24), Constâncio (2018), Broadbent (2018) and most of the studies we survey. However, this conclusion has been contested. As we discuss below, Filardo and Rungcharoenkitkul (2016), Gerdrup et al (2017) and Gourio, Kashyap and Sim (2017) argue that leaning against the wind can be worthwhile under some assumptions. Adrian and Liang (2018) emphasise the uncertainties involved. Finally, Borio (2016) and the Bank for International Settlements (BIS 2016) argue that more complicated analysis would yield different conclusions to the currently standard approach. We discuss many of these points of controversy and sensitivity below.
The new research has two complementary strands. One focuses on empirical estimates of relationships between interest rates, credit growth, financial crises and a small number of other variables. Examples include Habermeier et al (2015), Gorea et al (2016), Pescatori and Laséen (2016), Specchia and Plank (2017) and Svensson (2017a). A second ‘structural’ strand embeds these relationships into general equilibrium models with explicit preferences and technology. Examples include Ajello et al (2016), Alpanda and Ueberfeldt (2016), Gerdrup et al (2017), Gourio et al (2017), Aikman et al (2018) and Kockerols and Kok (2019). In this paper, we focus on the first strand, which is more transparent and facilitates comparisons to other empirical research. However, the two strands substantially overlap and most of our discussion also relates to the structural models.
Our paper is narrow in focus. As noted above, the papers we survey specify the benefit of leaning against the wind as avoiding substantial bank failures. Research has focused on these financial crises for several reasons. First, in contrast to some other dimensions of financial stability, there is substantial evidence that their occurrence is affected by monetary policy. Second, they are large and frequent enough to be important. Third, despite the previous point, they used to be rare enough to be omitted from central bank modelling. The third reason ceased to be convincing after the global financial crisis (GFC). Rectifying that neglect is now a major research priority.
However, there is more to financial stability than bank failures. The RBA (2016a) and Lowe (2017a, 2017b) have justified higher interest rates on the grounds that they reduce the fragility of household balance sheets. As far as we are aware, this argument has not been quantified in the research literature, so is outside our scope. That exclusion means that we ignore some potential benefits of leaning against the wind.
We also ignore some leading criticisms. Many commentators argue that interest rates are often not the best tool for addressing financial imbalances. Stronger prudential regulation, such as capital requirements or loan-to-value limits, might reduce risky lending with less collateral damage in the form of higher unemployment. See, for example, Yellen (2014), Bernanke (2015) or Broadbent (2018); for recent formal studies see Aikman et al (2018), Kockerols and Kok (2019) and references cited therein. Again, this is a controversial issue that this paper does not explore.
These limitations mean that our paper should not be viewed as a comprehensive assessment of leaning against the wind. Rather, we focus on one specific argument – that leaning against the wind might help to avoid financial crises. Most of the papers we survey believe this argument is the central issue at stake with leaning against the wind. However, as Lowe (2017b) discusses, other considerations might be relevant in some circumstances.
Another branch of research that we do not discuss examines the effect of debt, asset prices and financial frictions on the business cycle. These variables can have substantial effects on future spending decisions – for example, through the effect of net worth on consumption. Hence a forward-looking central bank will react to them. A common research finding is that augmenting a backward-looking Taylor rule with financial variables improves performance. Although this response is sometimes called ‘leaning against the wind’ others would consider it to be ‘normal inflation-targeting policy’. Again, this debate is outside our scope. Following Bernanke and Gertler (2000), our focus is on responses to financial variables over and above their effect on near-term forecasts of activity and inflation. The issue of leaning against the financial cycle (Filardo and Rungcharoenkitkul 2016) is more relevant and we discuss it Section 6.3.
2. A Simple Illustration
Table 1 provides a simple illustration of the issues, based on the IMF's survey of the international research (Habermeier et al 2015). As discussed below, this is a ‘back-of-the-envelope’ exercise. It integrates most of the relevant research in a simple, transparent way. However, as we discuss in subsequent sections, it ignores some important complications.
The IMF assumes a 100 basis point increase in interest rates is maintained for one year. A range of empirical estimates they survey suggests this would reduce the level of real debt by up to 0.3 to 2 per cent over a two to four year period, depending on the model. They estimate this would reduce the probability of a crisis, with a peak effect between 0.04 and 0.3 percentage points.[2] To present results favourable to leaning against the wind, row 1 of Table 1 shows the maximum of this range.
In the IMF's central scenario, the unemployment rate is assumed to be higher by 5 percentage points for six years in the event of a crisis (rows 2 and 3). We discuss this assumption in Section 3.5.
The estimated benefit of leaning against the wind, shown in row 4, is the product of the lower probability of a crisis, the unemployment gap in a crisis squared (assuming a quadratic loss function), and the duration of the crisis.
| Benefits | ||
| 1 | Lower crisis probability (percentage points) | 0.3 |
| 2 | Unemployment gap in crisis (percentage points) | 5 |
| 3 | Duration of crisis (years) | 6 |
| 4 | Benefits (0.3 × 52 × 6) / 100 | 0.45 |
| Costs | ||
| 5 | Unemployment gap (percentage points) | 0.5 |
| 6 | Duration of higher unemployment rate (years) | 4 |
| 7 | Costs (0.52 × 4) | 1.00 |
| 8 | Benefit-cost ratio | 0.45 |
|
Source: Habermeier et al (2015) |
||
Rows 5 and 6 show costs. The non-crisis unemployment rate increases by ½ percentage point, for a period of four years, in response to the higher policy rate, as estimated by the IMF's GIMF model. In row 7, the cost of leaning against the wind is calculated as the increase in the non-crisis unemployment gap squared, multiplied by the duration of this higher non-crisis unemployment rate.
Row 8 is the ratio of the estimated benefits to costs, 0.45. That is, the costs of leaning against the wind are likely to be about double the benefits. As noted above, this estimate assumes a large effect of interest rates on the crisis probability. The IMF emphasise alternative estimates, based on the average reduction in the probability of a crisis over time, which imply a benefit-cost ratio of 0.03.
3. Dynamic Estimates for Australia
A limitation of the simple approach used in Table 1 is that it ignores the evolution of costs and benefits over time. Because the elements interact multiplicatively and the loss function is quadratic the problem is highly nonlinear, so simple averages can be misleading. In this section, we show dynamic estimates for Australia which address this issue. We draw on the relevant research for each step in the argument, which comes from different sources and uses different methods. Joint estimation would be possible (Pescatori and Laséen (2016) is an example), however, we judged it to be more transparent and credible to use models and results that, where possible, have already been published and scrutinised. We also compare our estimates with others in the international literature. In general, the estimates seem to be similar, with differences being small and offsetting.
We show estimates over a nine-year horizon, the window most favourable to leaning against the wind. Assuming that monetary policy does not affect real variables in the long run, real credit growth would be above baseline (to get back to equilibrium) if the horizon were lengthened. That would reverse many of the effects shown below, driving the sum of total effects towards zero.
3.1 Interest Rate Assumption
To find a plausible profile for leaning against the wind, we take the difference between a forecast of the Australian economy in which interest rates evolve in line with market quotes and an optimal control scenario. The forecast based on market quotes closely resembles the forecast in the May 2016 Statement on Monetary Policy (RBA 2016b). The optimal control scenario sets interest rates so as to minimise the squared deviations of inflation from its target, the unemployment rate from the NAIRU, and squared changes in the policy rate. This optimal control exercise is much the same as those discussed in Stone, Wheatley and Wilkinson (2005, Section 3.3), Yellen (2012) and Haldane (2015). The key difference between the scenarios is that the forecast using market interest rates allows monetary policy to lean against the wind, whereas optimal control does not. Both scenarios are generated by the AUS-M model maintained by Outlook Economics.[3] The IMF (Habermeier et al 2017, p 46) provide and discuss similar estimates.
As shown in Figure 1A, this approach results in the cash rate being around 70 basis points higher for a period of a year, after which it declines to be around 25 basis points lower. We take this path of interest rates as given and examine the effects of leaning against the wind by this magnitude.
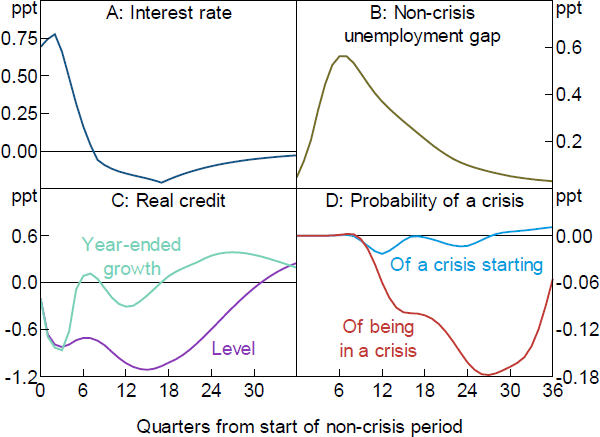
Sources: AUS-M; Authors' calculations; Jacobs and Rayner (2012); Schularick and Taylor (2012)
3.2 Response of the Non-crisis Unemployment Rate
The non-crisis unemployment gap is expected to increase by slightly more than ½ percentage point over a two-year period in response to the higher cash rate, before it gradually returns to its baseline level (Figure 1B). This estimate represents the difference between the unemployment rate projections in the ‘market path’ and ‘optimal control’ scenarios discussed above. AUS-M's estimate of the effect of interest rates on the rate of unemployment is slightly stronger than estimates for some other countries.[4] It is not clear whether this reflects differences between models or differences between countries. As with most macroeconometric models, AUS-M does not have a detailed financial sector, and so does not provide estimates of many of the other relationships in which we are interested. However, models of its type are a standard method of estimating the effect of interest rates on unemployment. For our purposes, they have the added advantage of providing consistent optimal control estimates.
Leaning against the wind affects many other variables that society cares about, such as inflation, income, the budget deficit and so on. Several papers use more comprehensive measures of costs. For example, Ajello et al (2016) and Pescatori and Laséen (2016) use a quadratic loss function that includes both the unemployment rate and inflation rate. However, if other variables move in line with unemployment, then both benefits and costs would increase proportionately and the ratio would be unchanged. The main challenge to this assumption is that crises may have permanent effects on output, which we discuss in Section 6.1.
3.3 Response of Real Credit
The baseline structural VAR described in Jacobs and Rayner (2012, pp 19–21) may provide the most authoritative estimates of the effect of real interest rates on credit in Australia.[5] This VAR implies that the 75 basis point increase in interest rates shown above would reduce the pace of growth of real credit by 0.9 percentage points after one year (Figure 1C). The pace of the decline slows as higher interest rates are unwound, and becomes positive once interest rates are below their baseline level. The level of real credit returns to its baseline level around eight years after the initial increase in interest rates. This response of credit is similar to or slightly larger than various international estimates. It is near the average of seven estimates surveyed by Gerdrup et al (2017, Table 1), that is, a 1 per cent increase in interest rates reduces credit by 1.35 per cent. Our estimated response is slightly larger than the estimates used by Svensson (2017a, Figure 3), and is near the upper end of a range of estimates in the international literature surveyed by the IMF (Habermeier et al 2015, fn 19). It is much larger than the ‘TOTEM’ and ‘Lens’ estimates reported by Gorea et al (2016, Figure 2) but somewhat smaller than their ‘MP2’ estimates.
We also experimented with other VARs used for operational work within the RBA. These are simpler than the model of Jacobs and Rayner (2012) and estimate a smaller effect of interest rates on credit. Results are available in the online supplementary information accompanying this paper. In order to show leaning against the wind in a more favourable light, we use the VAR that shows the larger effect.
The literature on leaning against the wind assumes that it is the growth in real credit that affects the probability of a banking crisis. Research underpinning that assumption is discussed in the following section. Alternatives to that assumption are discussed in Section 6.2.
3.4 Response of the Probability of a Crisis
The preferred model of Schularick and Taylor (2012) predicts the probability of a financial crisis starting as a function of five lags of annual real credit growth. According to this model, the probability of a crisis occurring in Australia has recently ranged from a peak of around 12 per cent in 1991 to 6 per cent in 2007 (prior to the GFC) and to a low in 2015 of about 3 per cent.[6] These estimates, particularly those for Australia before the crisis of the early 1990s and before the GFC for other countries, strike some as surprisingly low. That partly reflects a view that these crises were predicted beforehand by some observers. It may also reflect ‘hindsight bias’, the well-documented tendency to think that past events were more predictable than they actually were. See Wikipedia (2006) and references cited therein.
Schularick and Taylor's estimates seem to be fairly robust. Qualitatively similar results are obtained by the IMF (Habermeier et al 2015, p 17) for 35 advanced countries from 1960, by Babecký et al (2012) for 40 developed economies from 1970, by Gerdrup et al (2017) for 20 OECD countries since 1975, by Aikman et al (2018) for 23 developed countries since the 1980s, and by Kockerols and Kok (2019) for 22 European countries since 1970. There are considerable differences in specification and data measurement across these papers. They and others, such as Pescatori and Laséen (2016) or Svensson (2017a), conduct substantial sensitivity analysis.
For the purposes of assessing policy, it is the change in probability arising from new conditions, not the level, that matters. Schularick and Taylor's model, together with the lower credit growth discussed in the previous section, would imply that the quarterly probability of financial crises starting troughs at 0.02 percentage points below the baseline, as shown by the light blue line in Figure 1D.[7]
The ability of these models to predict financial crises, let alone changes in their probability, is very weak. But this does not mean the models are uninformative. We can confidently reject the hypothesis that the effects of changes in credit are large. If these effects were large, the models would have more explanatory power. A corollary of crises being unpredictable is that it is difficult to prevent them, although fostering resilience might be feasible.
The probability of being in a crisis (the red line in Figure 1D) represents the probabilities of a crisis starting in a given quarter, summed over the assumed duration of a crisis.[8] This troughs at 0.18 percentage points below the baseline. This is slightly larger (in magnitude) than the middle of the range of estimates reported by the IMF (Habermeier et al 2015, p 18), which range from −0.04 to −0.3 percentage points in response to a 1 percentage point interest rate increase.[9]
To put this in context, financial crises, as defined by Schularick and Taylor (2012), have occurred twice in Australia since 1870 – starting in 1893 and 1989. If we assume these crises lasted for six years, the unconditional probability of being in a crisis at any given point in time is 8.3 per cent. A reduction of 0.18 percentage points would lower that probability to 8.12 per cent. The tiny size of that change deserves emphasis. It implies that leaning against the wind is fairly ineffective at reducing the risks of financial crises. Its benefits are small – both relative to the costs of the policy (quantified below) and relative to the effects of other policies that might be employed (see, for example, Firestone, Lorenc and Ranish (2017)).
The small estimated effect of interest rates on the probability of financial crises has surprised many people. However, it is implied by central features of the data. Interest rates and credit growth vary over a wide range over the typical business cycle. So if interest rates or credit growth had substantial effects on the probability of a crisis then we would have experienced repeated episodes with a significant probability of a crisis. However, financial crises have been rare. In Australia they have been once-in-a-lifetime events.
3.5 Unemployment Gap in a Crisis
Figure 2 shows estimates of the change in unemployment during a financial crisis. The yellow line represents Australia from 1989[10], the blue line shows the United States from 2007 and the violet line shows average estimates by Gerdrup et al (2017, Figure 1) for a panel of 20 OECD countries from 1975 to 2014. We assume that in the event of a crisis the unemployment gap is 5 percentage points for six years, the same assumption the IMF made in Table 1 above. The IMF suggests this is representative of previous crises. This assumption, shown as the black line in Figure 2, describes a somewhat more severe crisis than the other estimates shown. Again, we choose parameters that favour leaning against the wind.
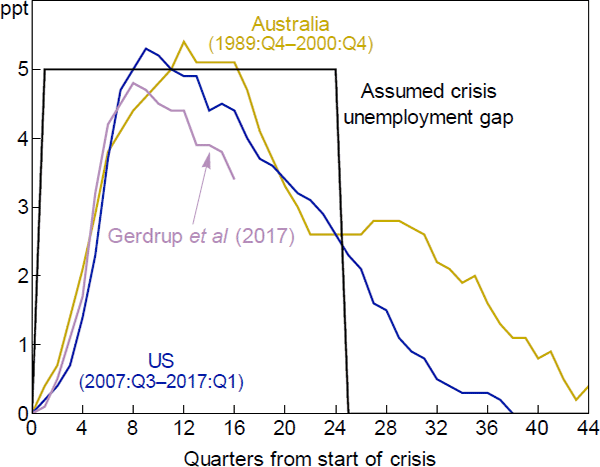
Sources: ABS; Authors' calculations; Federal Reserve Bank of St. Louis; Gerdrup et al (2017)
3.6 Comparing Costs with Benefits
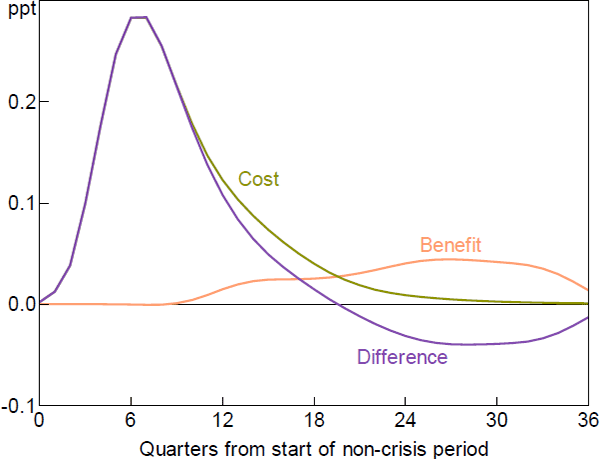
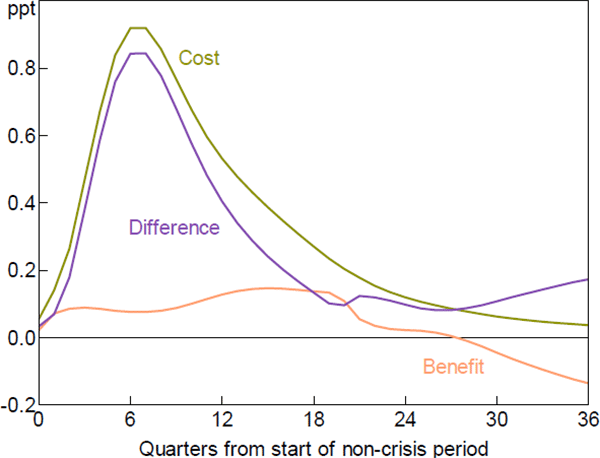
Figure 3 puts the above elements together. Expected loss is a probability-weighted average of the crisis and non-crisis losses. Appendix A shows how this loss can be decomposed into separate costs and benefits. The expected costs of leaning against the wind are given by Equation (A4) and represent the higher unemployment directly arising from higher interest rates (shown in Figure 1B), squared, with a small adjustment reflecting relative probabilities. Expected benefits are calculated using Equation (A5) and represent the increase in the squared unemployment gap in a crisis (that is, the difference between the assumed crisis unemployment gap – 5 percentage points – and the line in Figure 1B) multiplied by its lower probability (the red line in Figure 1D).
Figure 3 shows the flow of costs and benefits. We then sum these over a nine-year horizon, given most costs and benefits have accrued within this time frame. For simplicity, we assume the discount rate is zero. Our results are not very sensitive to alternative discount rates.
Both benefits and costs are in essentially the same units as in Table 1, so it is easy to compare Figure 3 with the IMF survey and the research on which it draws. The main difference between the dynamic and static estimates is that the response of the probability of a crisis, shown as the red line in Figure 1D, changes noticeably over time. In contrast, the estimate of the change in this probability in Table 1 is the peak effect of a range of estimates, which will overstate the benefits of leaning against the wind. This illustrates the benefit of a dynamic approach.
Nonetheless, the central result is the same as in the simple analysis of Table 1: costs greatly outweigh benefits. In the nine years following the initial increase in interest rates, the costs of leaning against the wind are estimated to be over three times larger than the benefits.
4. Alternative Parameters
5. Extensions
Results like those in Figure 3 are common and appear in various forms in different papers. However, they rest on some simplifying assumptions. In this section we discuss some complications. These generalise and make more realistic the earlier results without changing their essential character. Several of these extensions address criticisms of the simple approach. These criticisms can be quantified and they turn out not to change the conclusions.
5.1 Leaning against the Wind is More Desirable When Risks Are High
Many proponents of leaning against the wind call for it to be applied in response to rapid growth in credit or asset prices (e.g. Borio and Lowe 2002). As the name of the policy implies, it is selectively applied when risks are expected to be high. It is implicitly assumed that the benefit-cost ratio rises above 1 as financial risks increase.
The results in Sections 2 and 3 do not clearly assess such a policy, because the dependence of the estimates on financial conditions was not explicit. On a simple reading, many of the cost-benefit comparisons may appear to test whether leaning against the wind is either always desirable or never desirable. In this section we make underlying parameters conditional on financial conditions, to address the question ‘When is leaning against the wind desirable?’ Or, more bluntly, ‘Which wind?’
To be clear, the relevant question is not whether the probability of a crisis varies (though it does). To justify variations in policy over time, the response of costs or benefits to interest rates needs to vary. We focus on variations in the effect of interest rates on the probability of a crisis. Because interest rates operate through credit growth, this means the central question is whether the effect of credit on the probability of a crisis varies with financial conditions.
5.1.1 When real credit growth is high
Schularick and Taylor's (2012) preferred specification is a logit model. This is nonlinear, with interest rates having a larger effect on the probability of a crisis if real credit is growing at a faster pace. The aqua line in Figure 5 (left panel), labelled ‘Logit’, shows the marginal effect of the cash rate on the probability of a crisis, which becomes more negative as real credit growth increases.
The analysis underpinning Figure 3 estimated that a higher cash rate reduces the probability of being in a crisis by 0.2 percentage points at its peak, assuming that real credit growth was 5 per cent per annum over the previous five years. This is shown as the black dot, labelled ‘Baseline assumption’ in Figure 5 (left panel). Sensitivity analysis suggests that the benefits of leaning against the wind would exceed the costs if the effect on the probability of being in a crisis was doubled, peaking at –0.4 percentage points. This threshold is reached when real credit grows by around 15 per cent per year, shown as the aqua dot. As shown in the right panel of Figure 5, real credit has usually grown much slower than this threshold, though it briefly exceeded it in the late 1980s.
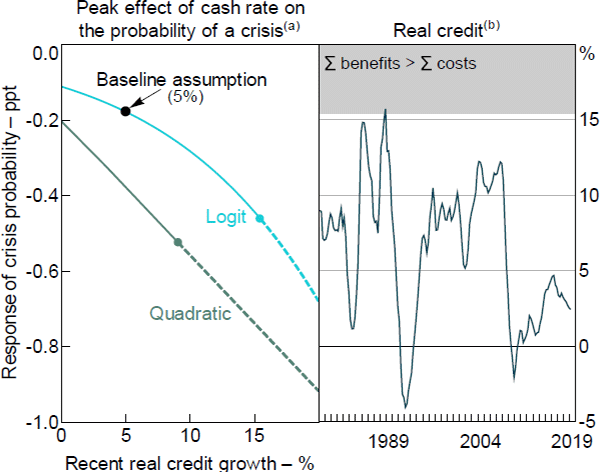
Notes:
(a) Estimates include Australia-specific intercepts (i.e. fixed effects); dashed lines represent rates of real credit growth for which the benefits of leaning against the wind exceed costs
(b) Year-ended growth
Sources: ABS; Authors' calculations; Schularick and Taylor (2012)
The nonlinearity in our estimates could reasonably be argued to be a result that is assumed rather than estimated, and that it is an accidental by-product of a functional form chosen for other reasons. However, a specification chosen so as to directly model the argument for nonlinear effects gives similar results. We estimate a least squares version of Schularick and Taylor's model, in which the probability of a crisis is a linear function of five lags of squared real credit growth.[11] These terms are jointly significant with a p-value of 6 per cent. That is, the statistical significance of these nonlinearities is marginal. The partial derivative of the probability of a crisis with respect to interest rates, shown as the dark aqua line in the left panel of Figure 5 (labelled ‘Quadratic’) then linearly decreases with credit growth. Although the quadratic specification is less plausible than the logistic, it has similar policy implications: leaning against the wind would be justified when credit growth is very high (for the quadratic specification, 9 per cent per year), well above current rates of growth.[12]
5.1.2 When the credit gap is high
A closely related hypothesis is that leaning against the wind is worthwhile when the credit-to-GDP ratio is high. This is one interpretation of the argument of the BIS (2016) that monetary policy should respond to ‘the financial cycle’. Borio (2016, p 5) argues that policy responses to the ‘cycle’ also apply to the credit gap, which is a major element of the BIS's cycle indicator. The credit gap is also a widely used early warning indicator of financial crises, and is required under the Basel III rules to be reported in the course of setting the countercyclical capital buffer (APRA 2015).
To assess whether leaning against the wind is more desirable when credit is high, we replace the squared terms in the least squares probability model of the previous section with both the level of the detrended credit-to-GDP ratio, or credit gap, and the product of the credit gap and real credit growth, both lagged two years. This interaction term allows the effect of real credit growth on the probability of a crisis – and hence the benefits of leaning against the wind – to increase linearly with the credit gap. The interaction term has a p-value of 4 per cent.[13] This effect is quantified in Figure 6, which shows the level of the credit gap on the left axis. The peak effect of the cash rate on the probability of a crisis is shown on the right axis. This is the same variable as shown in the left panel of Figure 5, however, as the effect is linear, we simply show this by rescaling the axis. Substituting this specification into the analysis underlying Figure 3, leaning against the wind would be worthwhile if the peak effect of the cash rate on the probability of a crisis was larger in magnitude than –0.6, which would occur if the credit-to-GDP ratio was 6 percentage points above trend, a level it last reached in 2003. We return to this issue in Section 6.3.
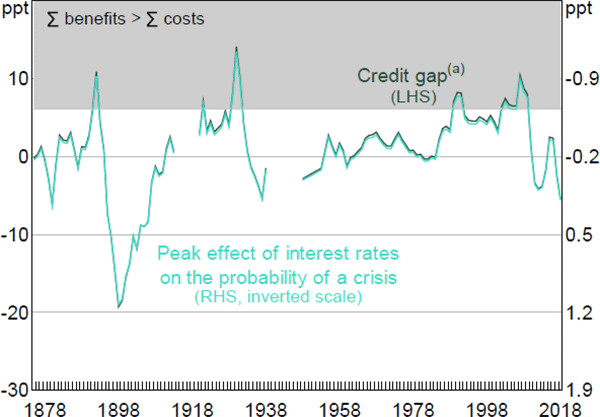
Note: (a) Deviation of credit-to-GDP ratio from one-sided HP trend with smoothing parameter of 1,562.5.; this is equivalent to the smoothing parameter of 400,000 recommended by the Basel Committee on Banking Supervision (BCBS) for quarterly data (Ravn and Uhlig 2002)
Sources: ABS; Authors' calculations; Schularick and Taylor (2012)
Higher interest rates reduce the probability of a crisis by lowering credit growth, which is estimated to have a larger effect on the probability of a crisis when the credit gap is higher. In principle, the credit gap could have further effects on the probability or severity of a crisis. We discuss these effects in Section 6.2.
5.2 Severity of the Crisis Depends on Policy
Sections 2 and 3 assumed that a crisis results in an unemployment gap of 5 percentage points, which was independent of other factors. However, as we discuss in this section, the severity of a crisis may be affected by a policy of leaning against the wind.
Svensson (2017a) suggests that a crisis is more likely to result in a fixed increase in the unemployment gap than a fixed level. Results shown in Figure 2 appear to be consistent with this. Starting from a higher pre-crisis unemployment gap, a crisis of a given size would result in a higher peak unemployment gap. Assuming increasing marginal costs (for example, quadratic loss), this increases the welfare cost of leaning against the wind. That is, the cost of leaning against the wind is not just a weaker economy if no crisis occurs, but a more costly crisis if it does occur.
Table 2 shows benefit-cost ratios based on some alternative assumptions that have been used in the literature. The first row represents our earlier estimates shown in Figure 3. The next row allows the severity of a crisis to depend on the pre-crisis unemployment gap. In Appendix B we explain how this effect, and others discussed below, can be estimated. Assuming that a crisis increases the unemployment gap by 5 percentage points (instead of to 5 percentage points) lowers the benefit-cost ratio to 0.07.
| Assumption | Benefit-cost ratio(a) | |
|---|---|---|
| 1 | Baseline: unemployment gap is 5 percentage points | 0.31 |
| 2 | Unemployment gap increases by 5 percentage points from the gap just before the crisis | 0.07 |
| 3 | Unemployment gap depends on recent credit growth | 0.62 |
| 4 | Unemployment gap depends on both pre-crisis unemployment gap and recent credit growth | 0.14 |
|
Notes: Appendix A shows how the total loss is decomposed into separate benefits and costs for each of these assumptions; |
||
In contrast, Gerdrup et al (2016) find that a crisis is likely to be more severe if real credit was growing strongly before the crisis. So by lowering credit growth, leaning against the wind is likely to decrease the severity, as well as the probability, of a crisis. For illustrative purposes, we use Gerdrup et al's estimates to gauge the relationship between credit growth and the severity of a crisis, shown in row 3 of Table 2. This increases the benefit-cost ratio to 0.62.
Row 4 and Figure 7 combine both assumptions. The severity of a crisis is much more affected by a higher initial unemployment gap than by slower growth of real credit. Allowing for both effects results in a benefit-cost ratio of 0.14; costs are eight times benefits. This is our preferred estimate.[14]
6. Criticisms and Doubts
A common criticism of the research on leaning against the wind is that more complicated analysis would generate different conclusions. We have partially addressed this criticism in Section 5, where we showed that some concerns about the research can be quantified and turn out not to change the conclusions.
Other objections are less easy to assess empirically. Some commentators object to the lack of microeconomic foundations. Others worry that parameter estimates relating to a one-off intervention would not apply to an ongoing policy. Others are concerned about interaction with other policies. And so on. For an extension of these criticisms see BIS (2016). For a rebuttal see Svensson (2016, Appendix K). We do not repeat all these debates here. In the following subsections we discuss three criticisms that we regard as especially serious.
6.1 ‘Financial Crises May Permanently Reduce Productivity’
Gourio et al (2017), BIS (2016) and Borio (2016) suggest that financial crises may cause permanent reductions in output, possibly by misallocating resources, reducing trust, severing financial intermediation networks and lowering the level of productivity.
There are examples that both support and challenge this view. Productivity accelerated following the financial crises in Australia in the 1990s[15] and the United States in the 1930s (Field 2003, 2012). However, it decelerated in many economies following the financial crisis of 2008 (on which, more below).
Formal research provides mixed results. A survey by the BCBS (2010, Annex 1) finds that banking crises are typically associated with huge long-lasting reductions in output. For example, the median estimate of the cumulative output loss is 63 per cent of annual pre-crisis GDP. However, some of the strongest research underlying this result is based on banking crises before the spread of deposit guarantees (e.g. Ramirez 2009) or under fixed exchange rates, and does not seem applicable to current institutional arrangements. Another difficulty is disentangling causation. In many cases a reduction in perceptions of longer-term growth rates causes the banking crisis, though Alfaro and Drehmann (2009) show that crises often arise from other reasons. Perhaps the most careful attempt to control for reverse causation is Cerra and Saxena (2008), who find that banking crises lower the long-run level of GDP by at least 4 per cent. In contrast, more recent research by Papell and Prodan (2012) finds little evidence that financial crises in advanced economies have long-term effects on either the level or the growth rate of GDP. In a detailed study of the recent US recovery, Fernald et al (2017, p 3) conclude that the growth in output has been relatively slow, but the shortfall was ‘largely—if not entirely—unrelated to the financial crisis’. Consistent with this, productivity growth has also slowed substantially in economies that did not suffer financial crises, such as Australia.
If one assumed that financial crises permanently lowered productivity, it would not follow that a longer-term analysis would show benefits of leaning against the wind. If monetary policy is neutral in the long run, leaning against the wind will not have a long-run effect on the level of real credit. The initial fall in real credit growth would eventually be followed by a period where credit growth is above its baseline level (and the probability of a crisis is higher), with the cumulative response summing to zero over the long run. Under standard assumptions, leaning against the wind simply shifts the probability of a crisis between periods, so that the undiscounted sum of benefits in the long run is approximately equal to zero.
Although it is difficult to say whether crises under current institutional arrangements would have permanent effects, evidence that effects are long-lasting is strong. Additional references include Terrones, Scott and Kannan (2009), Abiad et al (2009) and Reinhart and Rogoff (2014). This is reflected in our assumption that a representative crisis lasts for six years. This is in line with recent Australian and US financial crises, but well beyond the length of the average recession.
6.2 ‘Other Financial Variables are Excluded’
Another potential limitation of the cost-benefit comparisons is that the link between interest rates and the probability of a crisis occurring is assumed to be purely through real credit growth. However, interest rates may affect financial instability through different (and at least partly independent) channels. For example, empirical evidence suggests that changes in interest rates have an effect on the leverage of financial firms, risk-taking behaviour, asset prices and credit spreads.
These concerns raise two issues. First, if policy affects crises through other channels, then our focus on credit growth may understate total effects. Second, if other channels are important, then econometric regressions may suffer from omitted variables bias.
The results of Schularick and Taylor (2012, pp 1051–1052) support the assumption that the effect of interest rates on financial stability mainly occurs through credit growth. When they include real or nominal interest rates in addition to credit growth in their models predicting crises, they find that interest rate terms are insignificant or incorrectly signed[16] – suggesting that channels other than credit are unimportant. Some channels (such as ‘risk-taking’ or commercial property) are difficult to quantify. But were these channels important, their effect might be expected to be evident in the reduced form.
Perhaps the leading alternative channel of transmission is some transformation of the credit-to-GDP ratio, which Pescatori and Laséen (2016) and Drehmann et al (2010) find has significant predictive power for financial crises. However, as discussed in Section 5.1.2, when we include the detrended credit-to-GDP ratio in our model, it does not qualitatively change the cost-benefit comparison. Pescatori and Laséen find similar results with Canadian data (see Figure 4 above).
A difficulty with assigning the credit-to-GDP ratio a direct or important role is that it does not appear to be significantly affected by monetary policy. Although interest rates affect the numerator, credit (as discussed in Section 3.3), they have similar and hence offsetting effects on the denominator, nominal GDP. Empirical estimates of the sign are variable and of the magnitude are small. See Svensson (2013), Alpanda and Zubairy (2014), Robstad (2014), Habermeier et al (2015, p 15), Bank of Canada (2016, Box 7), Bauer and Granziera (2017) and Gelain, Lansing and Natvik (2018).
The absence of a clear or substantial effect of policy on the credit-to-GDP ratio surprises many observers. Interest rates work by changing the price of credit, so one might expect credit-sensitive expenditure to respond more strongly than other expenditure. But that does not mean the stock of credit (the numerator) changes faster than GDP. It takes several years for changes in expenditure flows to have a large effect on the stock.
In addition to raising the probability of a crisis, a large credit-to-GDP gap might increase its severity. However, there is little evidence suggesting this effect is clear or large (Habermeier et al 2015, p 17). Flodén (2014) finds that a 1 percentage point lower debt-to-income ratio results in only a small rise in the unemployment rate associated with a crisis of 0.02 percentage points.
Jordà, Schularick and Taylor (2015) find that ‘housing bubbles’ are highly significant (in addition to the effects of credit growth) in a logit model explaining recessions associated with financial crises.
Similarly, when we add five annual lags of real house price growth to the preferred model of Schularick and Taylor (2012) and estimate on Jordà et al's (2015) dataset, the house price terms are marginally significant with a p-value of 8 per cent. Anundsen et al (2016) present similar results for 20 OECD countries using quarterly data.
These results raise important issues. As we discussed earlier, interest rates have small effects on real credit growth and no clear effect on the credit-to-GDP ratio. However, they have large effects on house prices (Saunders and Tulip 2019). So a significant effect of house prices on financial stability offers the prospect of substantially raising the benefit of leaning against the wind. Despite that, Alpanda and Ueberfeldt (2016) examine ‘leaning against housing bubbles’ in a structural model calibrated to the Canadian economy and conclude that it lowers welfare. A further complication is that it is often thought to be the ‘bubble’ component of house prices that gives rise to financial instability, whereas interest rates determine the ‘fundamental’ component. Exploration of this issue is beyond the scope of this paper, though we consider it to be a leading area for future research.
Apart from the two exceptions discussed above, a wide-ranging search within the literature has not found alternatives to simple models with credit growth that better predict financial crises. This does not necessarily mean that other channels are not important in explaining financial instability. Instead, it could be that these other indicators of financial instability are highly correlated with credit growth, in which case credit growth would be a sufficient indicator for financial stability risks.
6.3 ‘Policy Should Lean against the Financial Cycle’
The BIS argues that the benefits of leaning against the wind increase with financial imbalances. As we show in Section 5.1.2, the net benefits of leaning against the wind are greatest when the detrended credit-to-GDP ratio is high. In this sense, the standard view can be extended so that monetary policy should ‘react to the cycle’.
Filardo and Rungcharoenkitkul (2016) provide alternative estimates in which ‘leaning against the financial cycle’ is worthwhile. An important factor underlying this conclusion is their estimate that a financial boom, as observed in the United States in 2006, gives rise to a probability of a ‘bust’ occurring of 10 to 20 per cent each quarter (their Figures 5 and 6). These estimates translate to a four-quarter-ahead probability of 35 to 60 per cent. A ‘bust’ is defined as a downtrend in the financial cycle indicator sufficient to drive output 4.5 per cent below potential.
These estimated probabilities are problematic for several reasons. They are an order of magnitude higher than other estimates of the probability of a financial crisis, such as Schularick and Taylor (2012), Habermeier et al (2015) or Pescatori and Laséen (2016).[17] However, that information is assumed to not affect asset prices, monetary policy or prudential supervision. The conclusions appear to be sensitive to these assumptions.
Filardo and Rungcharoenkitkul's (2016) approach is unusual in many ways and it is not clear which feature of their work explains why their probability estimates are so high. One possibility is that they estimate a large number of free parameters over a sample containing only three financial busts, leading to large ex post predictability or ‘overfitting’. Another possibility is that the financial cycle indicator is mean-reverting by construction, which naturally leads to large estimates of the conditional probability of a bust near the peaks of the financial cycle. Kockerols and Kok (2019) include the financial cycle in a more conventional model and find that costs of leaning against the wind are much greater than benefits.
In a closely related argument, Borio and the BIS emphasise the need for leaning against the wind to occur early, before the peak of the cycle. This argument rests on the assumption that changes in the cycle are persistent and predictable. They view this argument as a criticism of the standard approach, but we view it as addressing a separate question: specifically, when should monetary policy lean against the wind or, more precisely, in response to what? In contrast, our focus is on whether it should do so.
7. Conclusion
Evaluations of leaning against the wind are subject to substantial disagreement and uncertainty. Empirical evidence on some key assumptions is missing or thin. This is a subject of active research and conclusions may change. Two issues strike us as particularly troubling. First, some evidence points to banking crises as having highly persistent, if not permanent, effects on the level of productivity. Second, it is possible that interest rates affect the probability of a crisis through their effect on house prices, in addition to their effect through credit. Both these issues are priorities for further study. Nevertheless, the current state of the international research suggests that costs substantially outweigh benefits. Estimates for Australia lead to a similar conclusion.
However, that conclusion does not necessarily mean that the policy of leaning against the wind is inappropriate. Just because benefits of the policy cannot be identified or quantified does not mean they are small. Leaning against the wind might have benefits that are not apparent to researchers. In particular, the Reserve Bank has emphasised that low interest rates increase households' indebtedness and that this may have deleterious macroeconomic effects. Research on these issues is a priority.
Appendix A: Decomposition of Dynamic Estimates
This appendix provides details of how the change in social loss is decomposed into separate elements interpretable as benefits and costs. We assume the change in welfare can be represented by the following quadratic loss function.
where L is expected loss, is the expected welfare change as a result of leaning against the wind, u is the expected change in the non-crisis unemployment gap, c is the expected unemployment gap if a crisis occurs, and p is the probability of being in a crisis. The superscripts base and law represent the baseline and leaning against the wind scenarios, respectively. In other words, expected loss is a probability-weighted average of the crisis and non-crisis losses.
To simplify, assume that the non-crisis unemployment gap is zero in the baseline scenario, that is, ubase = 0. Then add and subtract and rearrange:
Crises under leaning against the wind are variable, so have a time subscript, whereas crises in the baseline are not. Equation (A2) can be rewritten in terms of costs and benefits.
where:
In addition to weighting factors, the expression COST represents the unemployment gap arising from leaning against the wind, BENEFIT represents the reduced probability of a crisis multiplied by the cost of the crisis (abstracting from the effect of policy on the crisis severity), and OTHER represents the difference in the size of a crisis that might arise under the two policies (this could be classified as either a cost or a benefit, depending on whether is greater or less than cbase).
In Section 3, we assume that , so that the unemployment gap in a crisis is the same regardless of previous policy. Then the term OTHER becomes zero and welfare loss is expressible as a simple difference between COST and BENEFIT, as shown in Figure 3. In Section 5.2 we relax this assumption. Implications and details are discussed in Appendix B.
Equations (A4) and (A5) are used to estimate the flow of costs and benefits. To make an assessment of whether leaning against the wind is desirable, we compare the cumulative sum of costs and benefits over the nine years following the initial change in interest rates.
Appendix B: Endogenous Crisis Severity
This appendix discusses how the cost-benefit results change if we assume the severity of a crisis is endogenous, as summarised in Section 5.2.
Svensson (2017a) assumes that a crisis results in a fixed increase in the unemployment gap, so that:
where cbase is now interpreted as the increase in the unemployment gap if a crisis occurs. Starting from a higher initial unemployment gap, , a crisis of a given size results in a higher peak unemployment gap. This means that a crisis is more costly if it occurs when the economy is already weak. This can be interpreted as an additional cost of leaning against the wind.
Gerdrup et al (2017) suggests that the crisis unemployment gap is likely to be smaller if leaning against the wind results in slower credit growth. This is partly based on the work of Jordà, Schularick and Taylor (2013), who find that credit-intensive expansions tend to be followed by deeper recessions. Jordà et al also find that credit-intensive expansions are substantially longer and larger, but we ignore this offset.
The effect of weaker credit growth on the severity of a crisis can be interpreted as an additional benefit of leaning against the wind. If we take into account both of these effects, the effect of leaning against the wind on the expected crisis unemployment gap can be expressed as:
By substituting Equation (B3) into Equation (A6), we have:
Equation (B4) can be separated into the cost of a higher initial unemployment gap (Svensson's assumption) and the benefit of weaker credit growth prior to the crisis (Gerdrup et al's assumption). When we do this, we can rewrite Equations (A3) to (A6) as follows.
where:
To quantify Svensson's argument we set the non-crisis unemployment gap equal to the path shown in Figure 1B and the amount by which the unemployment rate is assumed to increase in the crisis (cbase) equal to 5 percentage points. The sum of these represents a higher unemployment gap in a crisis under leaning against the wind. This raises the cost of the policy as defined in Equation (B6) and shown as the olive line in Figure B1. Benefits, shown as the light orange line, are largely unchanged from Figure 3. Costs are estimated to be almost 30 times larger than the benefits, the entry in Table 2, row 2.
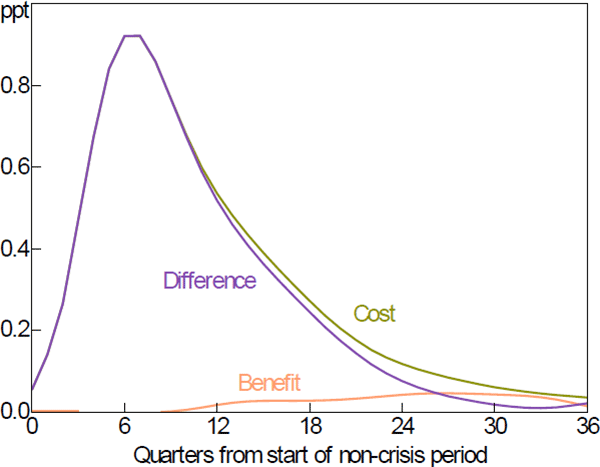
Figure B2 shows estimates of the increase in unemployment in a crisis for different assumptions about real credit growth over the previous five years, based on Gerdrup et al (2016, Table A3).[18] The dark red line assumes real credit grows at 5 per cent per year, as in our baseline. The light brown line assumes real credit grows 0.2 percentage points less each year, consistent with the effect of leaning against the wind shown in Figure 1C. Although Gerdrup et al's estimates indicate that credit has potentially large effects on crisis severity, the difference between the lines in Figure B2 is small, reflecting that interest rates have small effects on credit growth.
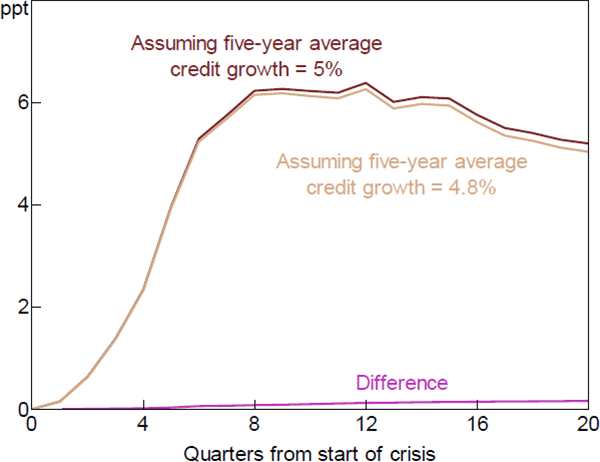
Sources: Authors' calculations; Gerdrup et al (2016)
We combine these estimates with our other parameters and Equations (B6) and (B7) to get overall costs and benefits as shown in Figure B3. Comparing this with Figure 3 shows that letting credit growth affect crisis severity substantially increases the benefits of leaning against the wind. However, the net benefit is still negative. This differs from Gerdrup et al, who found that allowing credit growth to affect the severity of a crisis makes leaning against the wind worthwhile. As Svensson (2017b) notes, the ‘black box’ nature of Gerdrup et al's estimates makes it difficult to explain differences. One partial explanation is that Gerdrup et al estimate the effect of credit growth on the probability of a crisis using data for 20 countries over the past 40 years. This provides larger estimates than those based on longer, narrower samples (see their Figure 8). Another partial explanation is that our estimates of the effect of interest rates on the unemployment rate are larger. This may reflect differences between Australian and Norwegian data. Svensson (2017b) provides more detailed comparisons of Gerdrup et al's results with others.
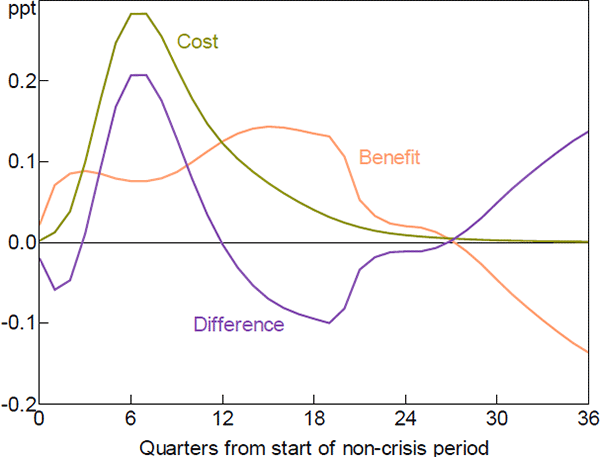
The costs of leaning against the wind far outweigh the benefits when we allow for both of these effects (Table 2; Figure 7). Importantly, taking into account both of these effects results in a larger expected welfare loss than in the baseline scenario. In other words, the increased costs from a higher initial unemployment gap are (much) larger than the benefits associated with a slower pace of real credit growth.
References
Abiad A, R Balakrishnan, P Keova Brooks, D Leigh and I Tytell (2009), ‘What's the Damage? Medium-Term Output Dynamics after Banking Crises’, IMF Working Paper No WP/09/245.
Adrian T and N Liang (2018), ‘Monetary Policy, Financial Conditions, and Financial Stability’, International Journal of Central Banking, 14(1), pp 73–131.
Aikman D, J Giese, S Kapadia and M McLeay (2018), ‘Targeting Financial Stability: Macroprudential or Monetary Policy?’, Bank of England Staff Working Paper No 734.
Ajello A, T Laubach, D López-Salido and T Nakata (2016), ‘Financial Stability and Optimal Interest-Rate Policy’, Board of Governors of the Federal Reserve System Finance and Economics Discussion Series No 2016-067.
Alfaro R and M Drehmann (2009), ‘Macro Stress Tests and Crises: What Can We Learn?’, BIS Quarterly Review, December, pp 29–41.
Allen F, C Bean and J De Gregorio (2016), ‘Independent Review of BIS Research: Final Report’, 23 December.
Alpanda S and A Ueberfeldt (2016), ‘Should Monetary Policy Lean against Housing Market Booms?’, Bank of Canada Staff Working Paper 2016-19.
Alpanda S and S Zubairy (2014), ‘Addressing Household Indebtedness: Monetary, Fiscal or Macroprudential Policy?’, Bank of Canada Working Paper 2014-58.
Anundsen AK, K Gerdrup, F Hansen and K Kragh-Sørensen (2016), ‘Bubbles and Crises: The Role of House Prices and Credit’, Journal of Applied Econometrics, 31(7), pp 1291–1311.
APRA (Australian Prudential Regulation Authority) (2015), ‘APRA Announces Countercyclical Capital Buffer Rate for ADIs’, Media Release No 15.38, 17 December.
Babecký J, T Havránek, J Matějů, M Rusnák, K Šmídková and B Vašíček (2012), ‘Banking, Debt, and Currency Crises: Early Warning Indicators for Developed Countries’, European Central Bank Working Paper Series No 1485.
Bank of Canada (2016), ‘Renewal of the Inflation-Control Target: Background Information – October 2016’.
Bauer GH and E Granziera (2017), ‘Monetary Policy, Private Debt, and Financial Stability Risks’, International Journal of Central Banking, 13(3), pp 337–373.
BCBS (Basel Committee on Banking Supervision) (2010), An Assessment of the Long-Term Economic Impact of Stronger Capital and Liquidity Requirements, Bank for International Settlements, Basel.
Bernanke BS (2015), ‘Should Monetary Policy Take into Account Risks to Financial Stability?’, Brookings Institution blog post, April 7, viewed 20 April 2017. Available at <https://www.brookings.edu/blog/ben-bernanke/2015/04/07/should-monetary-policy-take-into-account-risks-to-financial-stability/>.
Bernanke BS and M Gertler (2000), ‘Monetary Policy and Asset Price Volatility’, NBER Working Paper No 7559.
BIS (Bank for International Settlements) (2016), 86th Annual Report, BIS, Basel.
Borio C (2016), ‘Towards a Financial Stability-Oriented Monetary Policy?’, Presentation given at ‘Central Banking in Times of Change’ Conference on the occasion of the 200th anniversary of the OeNB, Vienna, 13–14 September.
Borio C and P Lowe (2002), ‘Asset Prices, Financial and Monetary Stability: Exploring the Nexus’, BIS Working Papers No 114.
Broadbent B (2018), ‘Monetary and Macroprudential Policies: The Case for a Separation of Powers’, in J Simon and M Sutton (eds), Central Bank Frameworks: Evolution or Revolution?, Proceedings of a Conference, Reserve Bank of Australia, Sydney, pp 209–226.
Cerra V and SC Saxena (2008), ‘Growth Dynamics: The Myth of Economic Recovery’, The American Economic Review, 98(1), pp 439–457.
Constâncio V (2018), ‘Financial Stability Risks and Macroprudential Policy in the Euro Area’, Address given at the 19th ‘The ECB and Its Watchers’ Conference, Frankfurt, 14 March.
Cusbert T and E Kendall (2018), ‘Meet MARTIN, the RBA's New Macroeconomic Model’, RBA Bulletin, March, viewed 15 March 2018. Available at <https://www.rba.gov.au/publications/bulletin/2018/mar/meet-martin-the-rbas-new-macroeconomic-model.html>.
Drehmann M, C Borio, L Gambacorta, G Jiménez and C Trucharte (2010), ‘Countercyclical Capital Buffers: Exploring Options’, BIS Working Papers No 317.
Fernald JG, RE Hall, JH Stock and MW Watson (2017), ‘The Disappointing Recovery of Output after 2009’, Brookings Papers on Economic Activity, Spring, pp 1–58.
Field AJ (2003), ‘The Most Technologically Progressive Decade of the Century’, The American Economic Review, 93(4), pp 1399–1413.
Field AJ (2012), A Great Leap Forward: 1930s Depression and U.S. Economic Growth, Yale Series in Economic and Financial History, Yale University Press, New Haven.
Firestone S, A Lorenc and B Ranish (2017), ‘An Empirical Economic Assessment of the Costs and Benefits of Bank Capital in the US’, Board of Governors of the Federal Reserve System Finance and Economics Discussion Series No 2017-034.
Filardo A and P Rungcharoenkitkul (2016), ‘A Quantitative Case for Leaning against the Wind’, BIS Working Papers No 594.
Flodén M (2014), ‘Did Household Debt Matter in the Great Recession?’, Supplement to blog post on ekonomistas.se, 16 February.
FOMC (Federal Open Market Committee) (2016), ‘Minutes of the Federal Open Market Committee, April 26–27, 2016’, Board of Governors of the Federal Reserve System, Washington DC.
Gelain P, KJ Lansing and G Natvik (2018), ‘Leaning against the Credit Cycle’, Journal of the European Economic Association, 16(5), pp 1350–1393.
Gerdrup KR, F Hansen, T Krogh and J Maih (2016), ‘Leaning against the Wind When Credit Bites Back’, Norges Bank Working Paper 9|2016.
Gerdrup KR, F Hansen, T Krogh and J Maih (2017), ‘Leaning against the Wind When Credit Bites Back’, International Journal of Central Banking, 13(3), pp 287–320.
Gorea D, O Kryvtsov and T Takamura (2016), ‘Leaning within a Flexible Inflation-Targeting Framework: Review of Costs and Benefits’, Bank of Canada Staff Discussion Paper 2016-17.
Gourio, F, AK Kashyap and J Sim (2017), ‘The Tradeoffs in Leaning against the Wind’, NBER Working Paper No 23658.
Habermeier K, T Mancini-Griffoli, G Dell'Ariccia and V Haksar (2015), ‘Monetary Policy and Financial Stability’, IMF Policy Paper, 28 August.
Haldane A (2015), ‘Drag and Drop’, Address given at The Biz Club lunch, Uppingham, 19 March.
Heibling T, P Karam, O Kamenik, D Laxton, H Wang and J Yao (2017), ‘Inflation Targeting in Australia: Performance, Challenges and Strategy Going Forward’, in ‘Australia: Selected Issues’, IMF Country Report No 17/43, pp 35–61.
Jacobs D and V Rayner (2012), ‘The Role of Credit Supply in the Australian Economy’, RBA Research Discussion Paper No 2012-02.
Jordà Ò, M Schularick and AM Taylor (2013), ‘When Credit Bites Back’, Journal of Money, Credit and Banking, 45(s2), pp 3–28.
Jordà Ò, M Schularick and AM Taylor (2015), ‘Leveraged Bubbles’, Journal of Monetary Economics, 76(Supplement), pp S1–S20.
Kockerols T and C Kok (2019), ‘Leaning against the Wind: Macroprudential Policy and the Financial Cycle’, European Central Bank Working Paper Series No 2223.
Lowe P (2017a), ‘Australia and Canada – Shared Experiences’, Address given to the Australia-Canada Economic Leadership Forum, Sydney, 22 February.
Lowe P (2017b), ‘Household Debt, Housing Prices and Resilience’, Address given to the Economic Society of Australia (QLD) Business Lunch, Brisbane, 4 May.
Papell DH and R Prodan (2012), ‘The Statistical Behavior of GDP after Financial Crises and Severe Recessions’, The B.E. Journal of Macroeconomics, 12(3), Article 2.
Pescatori A and S Laséen (2016), ‘Financial Stability and Interest-Rate Policy: A Quantitative Assessment of Costs and Benefits’, IMF Working Paper No WP/16/73.
Ramirez CD (2009), ‘Bank Fragility, “Money under the Mattress” and Long-Run Growth: US Evidence from the “Perfect” Panic of 1893’, Journal of Banking & Finance, 33(12), pp 2185–2198.
Ravn MO and H Uhlig (2002), ‘On Adjusting the Hodrick-Prescott Filter for the Frequency of Observations’, The Review of Economics and Statistics, 84(2), pp 371–376.
RBA (Reserve Bank of Australia) (2016a), ‘Minutes of the Monetary Policy Meeting of the Reserve Bank Board, Sydney – 6 December 2016’.
RBA (2016b), Statement on Monetary Policy, May.
Reinhart CM and KS Rogoff (2014), ‘Recovery from Financial Crises: Evidence from 100 Episodes’, The American Economic Review, 104(5), pp 50–55.
Robstad Ø (2014), ‘House Prices, Credit and the Effect of Monetary Policy in Norway: Evidence from Structural VAR Models’, Norges Bank Working Paper No 05|2014.
Saunders T and P Tulip (2019), ‘A Model of the Australian Housing Markets’, RBA Research Discussion Paper No 2019-01.
Schularick M and AM Taylor (2012), ‘Credit Booms Gone Bust: Monetary Policy, Leverage Cycles, and Financial Crises, 1870–2008’, The American Economic Review, 102(2), pp 1029–1061.
Specchia GL and D Plank (2017), ‘Is Reducing Financial Imbalances Worth the Short-Term Cost?’, ANZ Economic Insight – Australia, 5 July, ANZ Research.
Stone A, T Wheatley and L Wilkinson (2005), ‘A Small Model of the Australian Macroeconomy: An Update’, RBA Research Discussion Paper No 2005-11.
Sunstein CR (2018), The Cost-Benefit Revolution, MIT Press, Cambridge.
Svensson LEO (2013), ‘“Leaning against the Wind” Leads to a Higher (Not Lower) Household Debt-to-GDP Ratio’, Unpublished manuscript, Stockholm School of Economics, November. Available at <https://larseosvensson.se/files/papers/Leaning-against-the-wind-leads-to-higher-household-debt-to-gdp-ratio.pdf>.
Svensson LEO (2016), ‘Cost-Benefit Analysis of Leaning against the Wind: Are Costs Larger Also with Less Effective Macroprudential Policy?’, Paper presented at the Norges Bank Conference ‘Rethinking Inflation Targeting’, Oslo, 8–9 September. Available at <https://www.norges-bank.no/contentassets/3e9e16ea85e443598bb801484a01b42e/svensson.pdf>.
Svensson LEO (2017a), ‘Cost-Benefit Analysis of Leaning against the Wind’, Journal of Monetary Economics, 90, pp 193–213.
Svensson LEO (2017b), ‘Leaning against the Wind: Costs and Benefits, Effects on Debt, Leaning in DSGE Models, and a Framework for Comparison of Results’, International Journal of Central Banking, 13(3), pp 385–408.
Terrones ME, A Scott and P Kannan (2009), ‘From Recession to Recovery: How Soon and How Strong?’, World Economic Outlook: Crisis and Recovery, World Economic and Financial Surveys, IMF, Washington DC, pp 97–132.
Wikipedia (2006), ‘Hindsight Bias’, viewed 30 April 2019. Available at <https://en.wikipedia.org/wiki/Hindsight_bias>.
Yellen JL (2012), ‘The Economic Outlook and Monetary Policy’, Address given at the Money Marketeers of New York University, New York, 11 April.
Yellen JL (2014), ‘Monetary Policy and Financial Stability’, Inaugural Michel Camdessus Central Banking Lecture, International Monetary Fund, Washington DC, 2 July.
Acknowledgements
The authors would like to express our special gratitude to Matthew Read for detailed discussions on this topic. We also wish to thank Luci Ellis, Jonathan Kearns, Adam Gorajek, David Norman, David Orsmond, John Simon, Penny Smith, Stefano Tornielli di Crestvolant and participants at internal RBA seminars for helpful comments. The views expressed in this paper are those of the authors and do not necessarily reflect the views of the Reserve Bank of Australia. The authors are solely responsible for any errors.
Footnotes
Other prominent references include Schularick and Taylor (2012), who find that the probability of a financial crisis is positively correlated with the growth rate of real credit during the previous few years, and Drehmann et al (2010), who find that the detrended credit-to-GDP ratio is the best single predictor of financial crises. [1]
The IMF emphasise estimates of the average reduction in the probability of a crisis over time, which tend to be tiny. However, if one is summarising changing effects with a single number, peak effects may be more relevant given the nonlinearity of the loss function. [2]
Both scenarios use data as of April 2016. The AUS-M model is not publicly documented, however, its macroeconomic properties are essentially the same as those of the earlier TRYM model, discussed in detail at <http://archive.treasury.gov.au/contentitem.asp?NavId=016&ContentID=238>.
The RBA has developed a new macroeconometric model, MARTIN (see Cusbert and Kendall (2018)). Most of the work for this paper was done before MARTIN became operational.
[3]In response to a 100 basis point increase in the policy rate for a year, the IMF's GIMF model implies a peak increase in unemployment of somewhat less than ½ percentage point. The IMF (Habermeier et al 2015) describes this as broadly consistent with estimates from other models. The IMF's scenarios (for example, that shown in Table 1) assume this peak effect is constant for four years, implying a more persistent response than AUS-M. The Riksbank's DSGE model, Ramses, suggests that following a 100 basis point increase in the policy interest rate that is maintained for a year, Sweden's unemployment rate would also increase by about ½ percentage point after six quarters, before slowly falling back towards its baseline level (Svensson 2017a, Figure 1). These responses are somewhat weaker than that shown in Figure 1B given that the latter is in response to a 75 basis point interest rate change. [4]
This VAR includes gross national expenditure, GDP, inflation, the cash rate, interest rate differentials, real business credit, a survey measure of difficulty obtaining finance and the real exchange rate as endogenous variables, and major trading partner GDP, real commodity prices and real foreign interest rates as exogenous variables. The contemporaneous matrix is non-recursive. [5]
More detailed results are in our online supplementary information. Thanks to Matt Read for these calculations. [6]
This estimate uses the Australia-specific intercept, using Schularick and Taylor's online database and code (available at <http://economics.ucdavis.edu/people/amtaylor/files/CreditBoomsAER_data_replication.zip>), and assumes that real credit grows at 5 per cent a year in the absence of leaning against the wind, approximately the growth rate when we did this analysis (Figure 5, right panel). We discuss estimates conditional on other variables in Section 5.1. [7]
As discussed by Svensson (2017a, Appendix C), this is a linear approximation of the probability of a crisis, which is simple to calculate but results in slightly larger estimates of the crisis probability. A more thorough approach would be to model the probability of a crisis as a Markov process. [8]
Schularick and Taylor (2012), on which our results are based, describe a one standard deviation (7 percentage points) increase in real credit growth as increasing the incidence of financial crises by 2.8 percentage points. The estimates in Figure 1D are smaller because they reflect a much smaller change in credit growth (Figure 1C). [9]
Movements in the Australian unemployment rate to 1996 are perhaps more representative. After that, interest rates started to increase, signalling the beginning of a new business cycle. [10]
A possible issue with including squared real credit growth is that it does not distinguish between falls and increases in real credit. To address this issue, we have set the squared terms equal to zero when real credit growth is negative. [11]
The different levels of the lines in the left panel of Figure 5 are due to the low Australia-specific intercept, which depresses the marginal effect of interest rates in the logit equation but not in the linear probability model. Estimates from a logit model without country-specific intercepts are similar to the quadratic specification, with benefits equalling costs when real credit grows at 8 per cent. [12]
To avoid constraining the functional form, we also include the lagged credit gap as a separate regressor, which has a p-value of 46 per cent. Similar to the regression with squared credit growth, we restrict the interaction term to be zero when both the credit gap and real credit growth are negative. This restriction is not important; we get similar results if we use either the unrestricted interaction term in the regression, or if we add an arbitrary constant to the credit gap so that it is always positive. [13]
Figure 7 shows a negative ‘benefit’ after a period of seven years (the light orange line). This reflects the response of real credit to the assumed path for interest rates, which turns positive once interest rates are below their baseline level. The higher level of real credit growth increases the expected severity of a crisis, which is included as a negative benefit. [14]
GDP per hour worked grew by 1.1 per cent a year from 1980:Q1 to 1989:Q4 compared with 2.2 per cent from 1990:Q1 to 1999:Q4. [15]
Results for real interest rates are from Schularick and Taylor's online documentation, see footnote 7. [16]
For example, based on Schularick and Taylor's logit model (with fixed effects), the annual probability of a crisis starting in the United States in 2007 was 6 per cent. The highest estimated probability of a crisis starting in the United States was in 1957, at 10 per cent. [17]
These estimates differ from those shown in Figure 2 from Gerdrup et al (2017, Figure 1), reflecting small updates (which we do not incorporate) and different baseline credit growth for Australia relative to the OECD. [18]